列一元二次方程解下列应用题（每小题6分，共18分）
（1）已知两个正方形的面积之和为89，周长之差为12， 求这两个正方形的边长。
（2）有一人患了流感，经两轮传染后共有144人患了这种疾病，每轮传染中平均一个人传染了几人？
（3）据有关部门统计，我省农作物秸秆资源巨大，但合理利用量十分有限，2009年利用率只有30℅，大部分秸秆被直接焚烧，假定我省产生的农作物秸秆总量不变，且合理利用量的增长率相同，要使2011年的利用率提高到60℅，求每年的增长率。（可能用到的数据：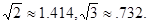
）
相关试题
如图，把直角三角形ABC的斜边AB放在直线L上，按顺时针方向在L上转动两次，使它转到△A″B″C″的位置上，设BC=1，AC=
，则顶点A运动到A′的位置时，点A经过的路线有多长，点A经过的路线与直线L所围成的面积有多大？
有一圆形的马戏帐篷，其半径为20m，从A到B有一笔直的栅栏，长为20
m．
（1）试求∠ACB的度数．
（2）某学校的学生在阴影区域里看马戏，设每平方米中有两个学生，试问该校有多少学生在看马戏？（
取3.14，取1.73）
的距离小于或等于
的所有点组成的图形．
的对角线
与
相交于点
，试说明点
，
，
在以
的长为半径的
上．
与墙
垂直，在地面的
处有一木柱，系着一匹马，已知系马的绳子的长度为
，试在图中画出马的活动区域．
相关知识点
推荐套卷
粤公网安备 44130202000953号