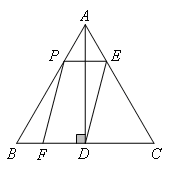
如图，在等边△ABC中，AB=6，AD⊥BC于点D，点P在边AB上运动，过点P作PE∥BC与边AC交于点E，连结ED，以PE、ED为邻边作□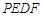
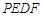，设□与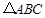
重叠部分图形的面积为
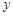，线段
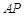的长为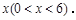
（1）求线段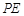
的长（用含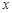
的代数式表示）；
（2）当四边形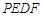为菱形时，求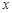的值；
（3）直接写出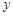与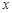之间的函数关系式；
×（－8）；
×(8－1
－0.04)；
－
+
－
)×36；
×2.4×
；相关知识点
推荐套卷
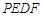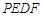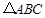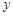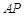如图，在等边△ABC中，AB=6，AD⊥BC于点D，点P在边AB上运动，过点P作PE∥BC与边AC交于点E，连结ED，以PE、ED为邻边作□，设□与重叠部分图形的面积为，线段的长为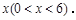
（1）求线段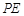的长（用含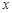的代数式表示）；
（2）当四边形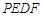为菱形时，求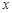的值；
（3）直接写出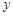与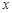之间的函数关系式；
粤公网安备 44130202000953号