某工厂生产一种机器的固定成本为5000元，且每生产100部，需要增加投入2500元，对销售市场进行调查后得知，市场对此产品的需求量为每年500部。已知年销售收入为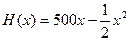
，其中x是产品售出的数量
。
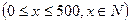（1
）若x为年产量，y 表示年利润，求
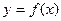的表达式。（年利
润=年销售收入—投资成本（包括固定成本））
（2）当年产量为何值时，工厂的年利润最大，其最大值是多少？
是曲线
上任意一点，求点
的最小距离。
；②
的导数
,且
,求不等式
的解集.
，
，又
，且
，
.求
，其中
，
；等差数列
，其中
，
.
（
为正整数），使得 
，
，相关知识点
推荐套卷
某工厂生产一种机器的固定成本为5000元，且每生产100部，需要增加投入2500元，对销售市场进行调查后得知，市场对此产品的需求量为每年500部。已知年销售收入为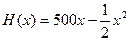，其中x是产品售出的数量。
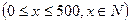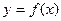（1）若x为年产量，y 表示年利润，求的表达式。（年利润=年销售收入—投资成本（包括固定成本））
（2）当年产量为何值时，工厂的年利润最大，其最大值是多少？
粤公网安备 44130202000953号