如图1,在 中,
中,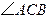 为锐角,点
为锐角,点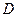 为射线
为射线 上一点,联结
上一点,联结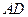 ,以
,以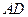 为一边且在
为一边且在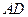 的右侧作正方形
的右侧作正方形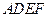 .
.
(1)如果 ,
,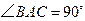 ,
,
①当点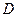 在线段
在线段 上时(与点
上时(与点 不重合),如图2,线段
不重合),如图2,线段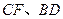 所在直线的位置关系为 __________ ,线段
所在直线的位置关系为 __________ ,线段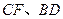 的数量关系为 ;
的数量关系为 ;
②当点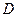 在线段
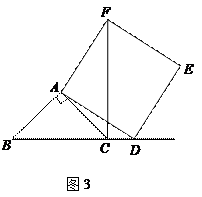
在线段 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
 |
|||||
 |
|||||
 |
|||||
(2)如果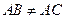 ,
, 是锐角,点
是锐角,点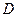 在线段
在线段 上,当
上,当 满足什么条件时,
满足什么条件时,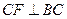 (点
(点 不重合),并说明理由.
不重合),并说明理由.
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号