（本小题满分12分）
已知椭圆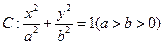
经过点M（-2，-1），离心率为
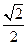。过点M作倾斜角
互补的两条直线分别与椭圆C交于异于M的另外两点P、Q。
（I）求椭圆C的方程；
（II）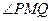
能否为直角？证明你的结论；
（III）证明：直线PQ的斜率为定值，并
求这个定值。
相关试题
型五方连块？
，其中
，且
．求
的最大值和最小值．
、
分别是
的外接圆和内切圆；证明：过
，都可作一个三角形
，使得
的外接圆和内切圆．
的所有排列
的集合为
；
，记
，
；求
．（其中
的元素个数）．
的最小值，使得存在以红点为顶点的推荐套卷
（本小题满分12分）
已知椭圆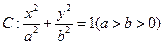经过点M（-2，-1），离心率为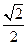。过点M作倾斜角
互补的两条直线分别与椭圆C交于异于M的另外两点P、Q。
（I）求椭圆C的方程；
（II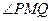）能否为直角？证明你的结论；
（III）证明：直线PQ的斜率为定值，并求这个定值。
粤公网安备 44130202000953号