若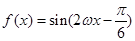 的图象关于直线
的图象关于直线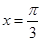 对称,其中
对称,其中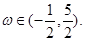
(1)求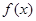 的解析式;
的解析式;
(2)将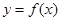 的图象向左平移
的图象向左平移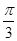 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到 的图象;若函数
的图象;若函数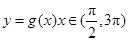 的图象与
的图象与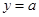 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求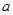 的值.
的值.
推荐套卷
若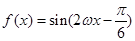 的图象关于直线
的图象关于直线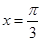 对称,其中
对称,其中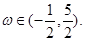
(1)求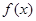 的解析式;
的解析式;
(2)将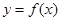 的图象向左平移
的图象向左平移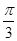 个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到
个单位,再将得到的图象的横坐标变为原来的2倍(纵坐标不变)后得到 的图象;若函数
的图象;若函数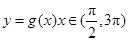 的图象与
的图象与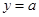 的图象有三个交点且交点的横坐标成等比数列,求
的图象有三个交点且交点的横坐标成等比数列,求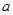 的值.
的值.