甲、乙两位篮球运动员进行定点投蓝，每人各投4个球，甲投篮命中的概率为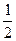
，乙投篮命中的概率为
．
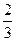(1)求甲至多命中2个且乙至少命中2个的概率；
(2)若规定每投篮一次命中得3分，未命中得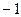
分，求乙所得分数
的概率分布和数学期望．
，
，求线段
的垂直平分线的方程．
和
的交点，且平行于直线
的直线方程．
的方程为
．
的取值范围．
在两坐标轴上的截距相等，且
到直线
，求直线
垂直，且在
轴上的截距比在
轴上的截距大2的直线方程．相关知识点
推荐套卷
甲、乙两位篮球运动员进行定点投蓝，每人各投4个球，甲投篮命中的概率为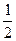，乙投篮命中的概率为．
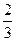(1)求甲至多命中2个且乙至少命中2个的概率；
(2)若规定每投篮一次命中得3分，未命中得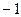分，求乙所得分数的概率分布和数学期望．
粤公网安备 44130202000953号