某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售
量可以增加，且每星期多卖出的商品件数与商品单价的降低值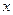
（单位：元，
）
的平方成正比，已知商品单价降低2元时，一星期多卖出24件．
（I）将一个星期的商品销售利润表示成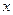的函数；
（II）如何定价才能使一个星期的商品销售利润最大？
相关试题
中各项均为正数，
是数列
项和，且
.
，试比较
与
的大小.
的对边长分别为a、b、c，已知a、b、c成等比数列，且
的大小；
，求函数
的值域.
的图象过点P（0,2）,且在点M
处的切线方程为
.
的解析式；（Ⅱ）求函数
为锐角，
，
，求
和
的值。
的前
项和为
，正数数列
的首项为
，
．记数列
前
．
，且
，使得
成等比数列？若存在，求出推荐套卷
某商品每件成本9元，售价为30元，每星期卖出432件，如果降低价格，销售
量可以增加，且每星期多卖出的商品件数与商品单价的降低值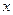（单位：元，）
的平方成正比，已知商品单价降低2元时，一星期多卖出24件．
（I）将一个星期的商品销售利润表示成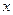的函数；
（II）如何定价才能使一个星期的商品销售利润最大？
粤公网安备 44130202000953号