（（本小题满分15分）
已知圆C过定点F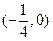
，且与直线
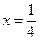相切，圆心C的轨迹为E，曲线E与直线
：
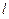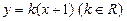相
交于A、B两点。
（I）求曲线E的方程；
（II）在曲线E上是否存在与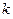
的取值无关的定点M，使得MA⊥MB？若存在，求出所有符合条件的定点M；若不存在，请说明理由。
，向量
，
，
, 其中
。
的单调增区间；
时，
的值。
且
与
的夹角为
，求
的值。
，
，求
的值。
，
的最小值为
，其
图像相邻的最
高点与最低点的横坐标之差为
，又
，求函数
·
+
·
。推荐套卷
（（本小题满分15分）
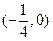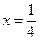已知圆C过定点F，且与直线相切，圆心C的轨迹为E，曲线E与直线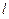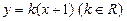：相交于A、B两点。
（I）求曲线E的方程；
（II）在曲线E上是否存在与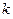的取值无关的定点M，使得MA⊥MB？若存在，求出所有符合条件的定点M；若不存在，请说明理由。
粤公网安备 44130202000953号