(本小题13分)已知函数 与
与 的图象相交于
的图象相交于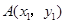 ,
,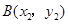 ,
, ,
,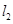 分别是
分别是 的图象在
的图象在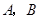 两点的切线,
两点的切线, 分别是
分别是 ,
,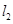 与
与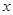 轴的交点.
轴的交点.
(1)求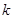 的取值范围;
的取值范围;
(2)设 为点
为点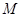 的横坐标,当
的横坐标,当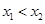 时,写出
时,写出 以
以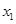 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(3)试比较 与
与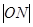 的大小,并说明理由(
的大小,并说明理由(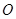 是坐标原点).
是坐标原点).
推荐套卷
(本小题13分)已知函数 与
与 的图象相交于
的图象相交于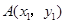 ,
,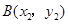 ,
, ,
,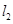 分别是
分别是 的图象在
的图象在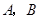 两点的切线,
两点的切线, 分别是
分别是 ,
,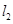 与
与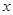 轴的交点.
轴的交点.
(1)求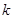 的取值范围;
的取值范围;
(2)设 为点
为点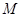 的横坐标,当
的横坐标,当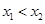 时,写出
时,写出 以
以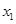 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(3)试比较 与
与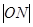 的大小,并说明理由(
的大小,并说明理由(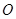 是坐标原点).
是坐标原点).