已知圆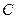 :
: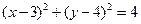
(1) 若平面上有两点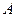 (1 , 0),
(1 , 0), (-1 , 0),点P是圆
(-1 , 0),点P是圆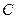 上的动点,求使
上的动点,求使 取得最小值时点
取得最小值时点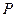 的坐标.
的坐标.
(2)若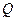 是
是 轴上的动点,
轴上的动点,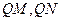 分别切圆
分别切圆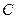 于
于 两点
两点
① 若 ,求直线
,求直线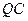 的方程;
的方程;
② 求证:直线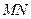 恒过一定点.
恒过一定点.
推荐套卷
已知圆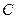 :
: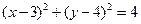
(1) 若平面上有两点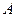 (1 , 0),
(1 , 0), (-1 , 0),点P是圆
(-1 , 0),点P是圆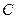 上的动点,求使
上的动点,求使 取得最小值时点
取得最小值时点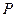 的坐标.
的坐标.
(2)若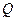 是
是 轴上的动点,
轴上的动点,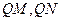 分别切圆
分别切圆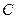 于
于 两点
两点
① 若 ,求直线
,求直线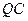 的方程;
的方程;
② 求证:直线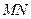 恒过一定点.
恒过一定点.