(11·肇庆)(本小题满分7分)
如罔7,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.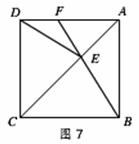
相关知识点
推荐套卷
(11·肇庆)(本小题满分7分)
如罔7,在一方形ABCD中.E为对角线AC上一点,连接EB、ED,
(1)求证:△BEC≌△DEC:
(2)延长BE交AD于点F,若∠DEB=140°.求∠AFE的度数.