在四棱锥P-ABCD中，底面ABCD是正方形，PD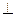
底面ABCD,M,N分别PA,BC的中点，且PD="AD=1" （12分)
(1)求证：MN∥平面PCD
(2)求证：平面PAC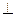平面PBD
(3)求MN与底面ABCD所成角的大小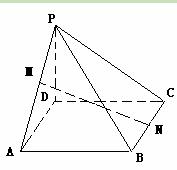
,且
、
是方程
的两个根.
的值;
，求△ABC的面积.
，
，求
的值．
满足
，
．
，求数列
的前
项和
．
、
、
为
的三内角，且其对边分别为
、
、
，若
．
，求
的最小正周期；
，
的值.推荐套卷
在四棱锥P-ABCD中，底面ABCD是正方形，PD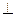底面ABCD,M,N分别PA,BC的中点，且PD="AD=1" （12分)
(1)求证：MN∥平面PCD
(2)求证：平面PAC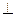平面PBD
(3)求MN与底面ABCD所成角的大小
粤公网安备 44130202000953号