(本小题满分16分) 一个三角形数表按如下方式构成:第一行依次写上n(n≥4)个数,在上一行的每相邻两数的中间正下方写上这两数之和,得到下一行,依此类推.记数表中第i行的第j个数为f(i,j).
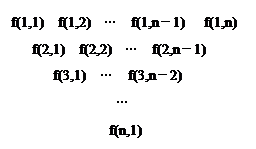
(1)若数表中第i (1≤i≤n-3)行的数依次成等差数列,求证:第i+1行的数也依次成等差数列;
(2)已知f(1,j)=4j,求f(i,1)关于i的表达式;
(3)在(2)的条件下,若f(i,1)=(i+1)(ai-1),bi= ,试求一个函数g(x),使得
Sn=b1g(1)+b2g(2)+…+bng(n)<,且对于任意的m∈(,),均存在实数,使得当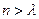 时,都有Sn >m.
时,都有Sn >m.