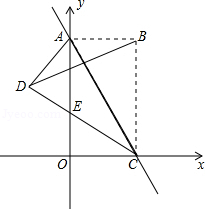
如图,将△ABC的顶点A放在⊙O上,现从AC与⊙O相切于点A(如图1)的
位置开始,将△ABC绕着点A顺时针旋转,设旋转角为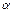 (0°<
(0°<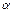 <120°),旋转后AC,AB
<120°),旋转后AC,AB
分别与⊙O交于点E,F,连接EF(如图2). 已知∠BAC=60°,∠C=90°,AC=8,⊙O的直
径为8.
(1)在旋转过程中,有以下几个量:①弦EF的长②弧EF的长③∠AFE的度数 ④点O到
EF的距离.其中不变的量是 (填序号);
(2)当BC与⊙O相切时,请直接写出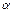 的值,并求此时△AEF的面积.
的值,并求此时△AEF的面积.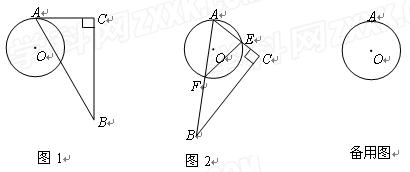
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号