(本题满分12分)为了防止受到核污染的产品影响我国民众的身体健康,某地要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为 ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为 ,每轮检测结果只有“合格”、“不
,每轮检测结果只有“合格”、“不 合格”两种,且两轮检测是否合格相互没有影响.
合格”两种,且两轮检测是否合格相互没有影响.
(Ⅰ)求该产品不能销售的概率;
(Ⅱ)如果产品可以销售,则每件产品可获利40元;如果产品不能销售,则每件产品亏损
80元(即获利 元).已知一箱中有产品4件,记一箱产品获利X元,求EX.
元).已知一箱中有产品4件,记一箱产品获利X元,求EX.
相关知识点
推荐套卷
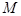 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中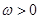 ,设
,设 (
( 为坐标原点).
为坐标原点). ,
,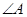 为
为 的内角,当
的内角,当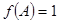 时,求
时,求 的值域为集合
的值域为集合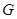 ,不等式
,不等式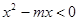 的解集为集合
的解集为集合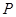 .当
.当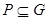 时,求实数
时,求实数 的最大值.
的最大值. ,点
,点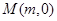 在x轴的正半轴上,过点M的直线
在x轴的正半轴上,过点M的直线 与抛物线C相交于A,B两点,O为坐标原点.
与抛物线C相交于A,B两点,O为坐标原点.
 ,且直线
,且直线 恒为定值?
恒为定值? 经过点
经过点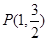 ,离心率
,离心率 .
. 与椭圆C交于A,B两点,若AB的中点M在抛物线E:
与椭圆C交于A,B两点,若AB的中点M在抛物线E: 上,求直线
上,求直线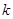 的取值范围.
的取值范围. ,双曲线
,双曲线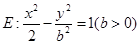 .
.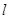 与双曲线E的其中一条渐近线平行,求双曲线E的离心率;
与双曲线E的其中一条渐近线平行,求双曲线E的离心率;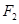 ,与双曲线交于P、Q两点,且
,与双曲线交于P、Q两点,且 ,求双曲线方程.
,求双曲线方程. 的距离比到点M到直线
的距离比到点M到直线 的距离小4.
的距离小4.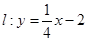 对称,求直线AB的方程.
对称,求直线AB的方程. 粤公网安备 44130202000953号
粤公网安备 44130202000953号