(本小题满分12分)
某玩具厂计划每天生产A、B、C三种玩具共100个. 已知生产一个玩具A需5分钟,生产一个玩具B需7分钟,生产一个玩具C需4分钟,而且总生产时间不超过10个小时. 若每生产一个玩具A、B、C可获得的利润分别为5元、6元、3元.
(I)用每天生产的玩具A的个数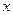 与玩具B的个数
与玩具B的个数 表示每天的利润
表示每天的利润 元;
元;
(II)请你为玩具厂制定合理的生产任务分配计划,使每天的利润最大,并求最大利润.
相关知识点
推荐套卷
(本小题满分12分)
某玩具厂计划每天生产A、B、C三种玩具共100个. 已知生产一个玩具A需5分钟,生产一个玩具B需7分钟,生产一个玩具C需4分钟,而且总生产时间不超过10个小时. 若每生产一个玩具A、B、C可获得的利润分别为5元、6元、3元.
(I)用每天生产的玩具A的个数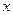 与玩具B的个数
与玩具B的个数 表示每天的利润
表示每天的利润 元;
元;
(II)请你为玩具厂制定合理的生产任务分配计划,使每天的利润最大,并求最大利润.