（本小题满分12分）
设函数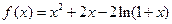
.
(1)求函数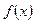
的单调区间；
(2)当
时,是否存在整数
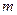，使不等式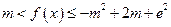
恒成立？若
存在，求整数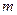的值；若不存在，请说明理由。
(3)关于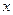
的方程
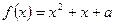在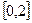
上恰有两个相异实根,求实数
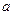的取值范围。
相关试题
的离心率为
，点
是双曲线的一个顶点．
作倾斜角为30°直线
，直线
两点,求
的长．
:
，命题
: 对任何
R，都有
，命题
的取值范围．
，
，则“
，或
”是“
”的什么条件？
，且
，
，
，使得
在
上为减函数，并且在
上为增函数，若不存在，说明理由.
时，求
.
对任意
,都有
, 
且当
时，都有
.
上单调递减.推荐套卷
（本小题满分12分）
设函数.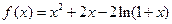
(1)求函数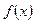的单调区间；
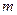(2)当时,是否存在整数，使不等式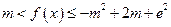恒成立？若
存在，求整数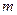的值；若不存在，请说明理由。
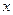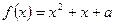(3)关于的方程在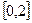上恰有两个相异实根,求实数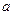的取值范围。
粤公网安备 44130202000953号