如图,互相垂 直的两条公路
直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个
,现欲将其扩建成一个 更大的三角形花园
更大的三角形花园 ,要求
,要求 在射线
在射线 上,
上, 在射线
在射线 上,且
上,且 过点
过点 ,其中
,其中 米,
米,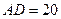 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为 .
.
(1)设

 米,将
米,将 表示成
表示成 的函数.
的函数.
(2) 当
当 的长度是多少时,
的长度是多少时, 最小?并求
最小?并求 的最小值.
的最小值.
(3)要使 不小于
不小于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?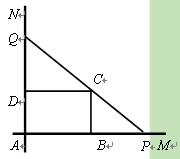
推荐套卷
如图,互相垂 直的两条公路
直的两条公路 、
、 旁有一矩形花园
旁有一矩形花园 ,现欲将其扩建成一个
,现欲将其扩建成一个 更大的三角形花园
更大的三角形花园 ,要求
,要求 在射线
在射线 上,
上, 在射线
在射线 上,且
上,且 过点
过点 ,其中
,其中 米,
米,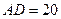 米. 记三角形花园
米. 记三角形花园 的面积为
的面积为 .
.
(1)设

 米,将
米,将 表示成
表示成 的函数.
的函数.
(2) 当
当 的长度是多少时,
的长度是多少时, 最小?并求
最小?并求 的最小值.
的最小值.
(3)要使 不小于
不小于 平方米,则
平方米,则 的长应在什么范围内?
的长应在什么范围内?