如图，
为
外接圆的切线，
的延长线交直线
于点
分别为弦
与弦
上的点，且
四点共圆.
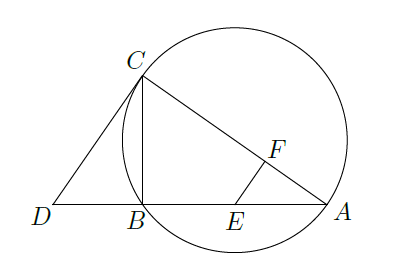
（Ⅰ）证明：
是
外接圆的直径；
（Ⅱ）若
,求过
四点的圆的面积与
外接圆面积的比值.
中，以
轴为始边做两个锐角
,
，它们的终边分别与单位圆相交于
两点，已知点
的横坐标为
，点
的纵坐标为
.
的值；
的值．
，
（其中A＞0，
＞0，
＜
的部分图象如图所示，求这个函数的解析式.
为原点，
.
的坐标及
；
，求
及
的坐标；
.
按下列条件求
值。
； （2）
.
试判断
三点的位置关系.推荐套卷
如图，
为
外接圆的切线，
的延长线交直线
于点
分别为弦
与弦
上的点，且
四点共圆.
（Ⅰ）证明：
是
外接圆的直径；
（Ⅱ）若
,求过
四点的圆的面积与
外接圆面积的比值.
粤公网安备 44130202000953号