小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA= ,sinA′=
,sinA′= .
.
⑴求此重物在水平方向移动的距离BC;
⑵求此重物在竖直方向移动的距离B′C.(结果保留根号)
相关知识点
推荐套卷
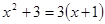 ;
;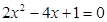 .
. 年仍保持相同的年平均增长率,请你预测
年仍保持相同的年平均增长率,请你预测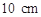 ,宽为
,宽为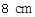 的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)的面积是原矩形面积的80%,求所截去的小正方形的边长.
的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)的面积是原矩形面积的80%,求所截去的小正方形的边长.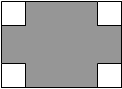
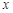 的方程
的方程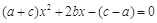 的两根之和为
的两根之和为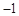 ,两根之差为1,其中
,两根之差为1,其中 是△
是△ 的三边长.
的三边长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号