如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q 作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
(1)求点D到BC的距离 ;
;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR是以PQ为一腰的等腰三角形?若存在,请求出所有满足要求的 x的值;若不存在,请说明理由
x的值;若不存在,请说明理由
 |
相关知识点
推荐套卷
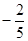 x2+
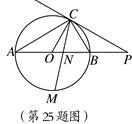
x2+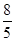 x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.
x+2交x轴于A、B两点(点A在点B的左侧),与y轴交于点C.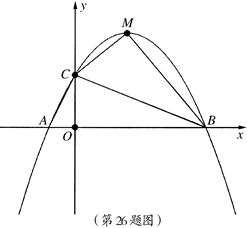
 AB;
AB; 元,要使(2)中所有方案获利相同,
元,要使(2)中所有方案获利相同, 粤公网安备 44130202000953号
粤公网安备 44130202000953号