已知在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8.E,F分别是线段A1A,BC上的点.
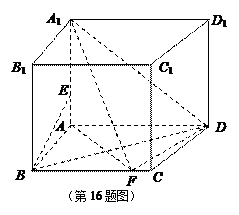
(1)若A1E=5,BF=10,求证:BE∥平面A1FD.
(2)若BD⊥A1F,求三棱锥A1-AB1F的体积.
相关知识点
推荐套卷
已知在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,且满足AD⊥AB,BC∥AD,AD=16,AB=8,BB1=8.E,F分别是线段A1A,BC上的点.
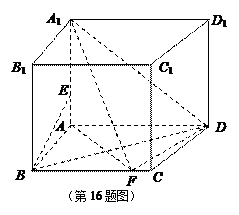
(1)若A1E=5,BF=10,求证:BE∥平面A1FD.
(2)若BD⊥A1F,求三棱锥A1-AB1F的体积.