如图，四棱锥S－ABCD的所有棱长均为1米，一只小虫从S点出发沿四棱锥爬行，若在每顶点处选择不同的棱都是等可能的．设小虫爬行n米后恰回到S点的概率为Pn(n≥2，n∈N)．
(1)求P2，P3的值；
(2)求证：3Pn＋1＋Pn＝1(n≥2，n∈N)；
(3)求证：P2＋P3＋…＋Pn＞(n≥2，n∈N)．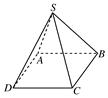
在定义域上单调递增；命题Q不等式
对任意实数
恒成立若
是真命题，求实数
的取值范围
，
，
，
，
，你能得到一个怎样的一般不等式？并加以证明．
的单调区间； 
对任意
成立，求实数
的取值范围。
≤
(x＞0，y＞0)恒成立的
是定义在（0，＋∞）上的单调增函数，满足:
恒有
，求：
；
，求
的取值范围。推荐套卷
如图，四棱锥S－ABCD的所有棱长均为1米，一只小虫从S点出发沿四棱锥爬行，若在每顶点处选择不同的棱都是等可能的．设小虫爬行n米后恰回到S点的概率为Pn(n≥2，n∈N)．
(1)求P2，P3的值；
(2)求证：3Pn＋1＋Pn＝1(n≥2，n∈N)；
(3)求证：P2＋P3＋…＋Pn＞(n≥2，n∈N)．
粤公网安备 44130202000953号