（本小题满分12分）
已知椭圆C：
（a>b>0）的离心率为
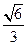，其左、右焦点分别是F1、F2，点P是坐标平面内的一点，且｜OP｜＝
，
·
＝
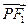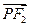（点O为坐标原点）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线y＝x与椭圆C在第一象限交于A点，若椭圆C上两点M、N使
＋
＝
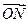λ
，λ∈（0，2）求△OMN面积的最大值．
相关试题
推荐套卷
（本小题满分12分）
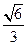已知椭圆C：（a>b>0）的离心率为，其左、右焦点分别是F1、F2，点P是坐标平面内的一点，且｜OP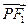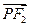｜＝，·＝（点O为坐标原点）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）直线y＝x与椭圆C在第一象限交于A点，若椭圆C上两点M、N使＋＝
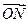λ，λ∈（0，2）求△OMN面积的最大值．
粤公网安备 44130202000953号