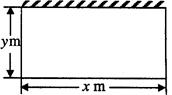
某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为 元
元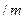 , 两侧的造价为
, 两侧的造价为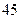 元
元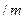 , 顶部的造价为
, 顶部的造价为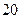 元
元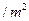 . 设仓库正面的长为
. 设仓库正面的长为 , 两侧的长各为
, 两侧的长各为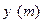 .
. 
(1)用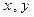 表示这个仓库的总造价
表示这个仓库的总造价 (元);
(元);
(2)若仓库底面面积
 时, 仓库的总造价
时, 仓库的总造价 最少是多少元,
最少是多少元,
此时正面的长应设计为多少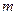 ?
?
推荐套卷
某单位计划建一长方体状的仓库, 底面如图, 高度为定值. 仓库的后墙和底部不花钱, 正面的造价为 元
元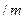 , 两侧的造价为
, 两侧的造价为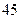 元
元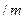 , 顶部的造价为
, 顶部的造价为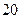 元
元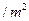 . 设仓库正面的长为
. 设仓库正面的长为 , 两侧的长各为
, 两侧的长各为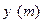 .
. 
(1)用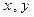 表示这个仓库的总造价
表示这个仓库的总造价 (元);
(元);
(2)若仓库底面面积
 时, 仓库的总造价
时, 仓库的总造价 最少是多少元,
最少是多少元,
此时正面的长应设计为多少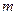 ?
?