(12分) 一副扑克牌共52张(除去大小王)，规定：
①J、Q、 K、A算1点;
②每次抽取一张，抽到被3整除的点数奖励5元，抽到黑桃A奖励50元；
③如未中奖,则抽奖人每次付出5元。
现有一人抽奖2次(每次抽后放回)，
（1）求这人不亏钱的概率；
（2）设这人输赢的钱数为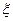
，求
。
相关试题
（n∈N*）,它的前n项和为
，且
求数列
+
的最小值；
+
+
的最小值．
时，求f（x）的极值点；
+
=1有相同焦点，且经过点（4，
）．推荐套卷
(12分) 一副扑克牌共52张(除去大小王)，规定：
①J、Q、 K、A算1点;
②每次抽取一张，抽到被3整除的点数奖励5元，抽到黑桃A奖励50元；
③如未中奖,则抽奖人每次付出5元。
现有一人抽奖2次(每次抽后放回)，
（1）求这人不亏钱的概率；
（2）设这人输赢的钱数为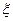，求。
粤公网安备 44130202000953号