第四届中国国际航空航天博览会于2010年11月在珠海举行，一次飞行表演中，一架直升飞机在海拔800m的高度飞行，从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°（如右图所示）.
（1）试计算这个海岛的宽度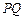
.
（2）若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为45°和30°，他们估计P、Q两处距离大约为600m，由此试估算出观测者甲（在P处）到飞机的直线距离.
相关试题
．
，求
的取值范围；
的最值
，并给出取最值时对应的
的值
数
的定义域；
上的奇函数
是减函数，若
，求实数
的取值范围．
，
，求
，
，
，
．
，求数列{cn}的前n项和Tn.推荐套卷
第四届中国国际航空航天博览会于2010年11月在珠海举行，一次飞行表演中，一架直升飞机在海拔800m的高度飞行，从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°（如右图所示）.
（1）试计算这个海岛的宽度.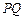
（2）若两观测者甲、乙分别在海岛两侧海岸P、Q处同时测得飞机的仰角为45°和30°，他们估计P、Q两处距离大约为600m，由此试估算出观测者甲（在P处）到飞机的直线距离.
粤公网安备 44130202000953号