．（本小题满分12分）
如图所示，有公共边的两正方形ABB1A1与BCC1B1的边AB、BC均在平面α内，且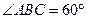
，M是BC的中点，点N在C1C上。
（1）试确定点
N的位置，使
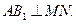
（2）当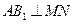
时，求二面角M—AB1—N的余弦值。
相关试题
a
b，
2a
3（a- b）。求证：A、B、D三点共线；
，使
，
满足
是公差为
的等差数列.当
时,求
的值;
求正整数
使得一切
均有
中，内角
对边的边长分别是
，已知
，
．
，求
；
，求
，若存在不同时为
的实数
和
，使
且
，试求函数关系式
推荐套卷
．（本小题满分12分）
如图所示，有公共边的两正方形ABB1A1与BCC1B1的边AB、BC均在平面α内，且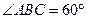，M是BC的中点，点N在C1C上。
（1）试确定点N的位置，使
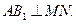
（2）当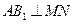时，求二面角M—AB1—N的余弦值。
粤公网安备 44130202000953号