（（本小题满分13分）
甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.
（Ⅰ）求选出的4名选手均为男选手的概率.
（Ⅱ）记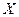
为选出的4名选手中女选手的人数，求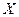的分布列和期望.
的顶点
，求
的内角平分线
所在的直线方程
，求直线
的方程。
过点
且与以
为端点的线段相交，求直线
与
轴的交点为
，把直线
绕点
，推荐套卷
（（本小题满分13分）
甲班有2名男乒乓球选手和3名女乒乓球选手，乙班有3名男乒乓球选手和1名女乒乓球选手，学校计划从甲乙两班各选2名选手参加体育交流活动.
（Ⅰ）求选出的4名选手均为男选手的概率.
（Ⅱ）记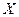为选出的4名选手中女选手的人数，求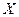的分布列和期望.
粤公网安备 44130202000953号