（本小题满分12分）
如图：四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB＝90°，PA⊥平面ABCD，PA=BC=1，AB=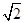
,F是BC的中点．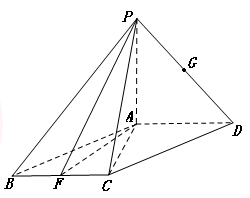
（Ⅰ）求证：DA⊥平面PAC；
（Ⅱ）点G为线段PD的中点，证明CG∥平面PAF；
（Ⅲ）求三棱锥A—CDG的体积．
化为
进制的数.推荐套卷
（本小题满分12分）
如图：四棱锥P-ABCD中，底面ABCD是平行四边形，∠ACB＝90°，PA⊥平面ABCD，PA=BC=1，AB=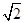,F是BC的中点．
（Ⅰ）求证：DA⊥平面PAC；
（Ⅱ）点G为线段PD的中点，证明CG∥平面PAF；
（Ⅲ）求三棱锥A—CDG的体积．
粤公网安备 44130202000953号