某种植企业同时培育甲、乙两个品种杉树幼苗,甲品种杉树幼苗培育成功则每株利润80元,培育失败,则每株亏损20元;乙品种杉树幼苗培育成功则每株获利润150元,培育失败,则每株亏损50元。统计数据表明:甲品种杉树幼苗培育成功率为90%,乙品种杉树幼苗培育成功率为80%。假设每株幼苗是否培育成功相互独立。
(I)求培育3株甲品种杉树幼苗成功2株的概率;
(II)记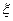 为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求
为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求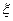 的分布列及其期望。
的分布列及其期望。
推荐套卷
某种植企业同时培育甲、乙两个品种杉树幼苗,甲品种杉树幼苗培育成功则每株利润80元,培育失败,则每株亏损20元;乙品种杉树幼苗培育成功则每株获利润150元,培育失败,则每株亏损50元。统计数据表明:甲品种杉树幼苗培育成功率为90%,乙品种杉树幼苗培育成功率为80%。假设每株幼苗是否培育成功相互独立。
(I)求培育3株甲品种杉树幼苗成功2株的概率;
(II)记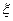 为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求
为培育1株甲品种杉树幼苗与1株乙品种杉树幼苗可获得的总利润,求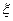 的分布列及其期望。
的分布列及其期望。