已知关于x的函数f(x)＝
＋bx2＋cx＋bc,其导函数为f+(x).令g(x)＝∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x＝1处有极值-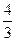
，试确定b、c的值：
（Ⅱ）若∣b∣>1,证明对任意的c,都有M>2: 
(Ⅲ)若M≧K对任意的b、c恒成立，试求k的最大值。
与已知圆
的交点，且在两坐标轴上的四个截距之和为8的圆的方程。
的单调性，并求其值域。
的定义域。
（2）
推荐套卷
已知关于x的函数f(x)＝＋bx2＋cx＋bc,其导函数为f+(x).令g(x)＝∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x＝1处有极值-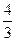，试确定b、c的值：
（Ⅱ）若∣b∣>1,证明对任意的c,都有M>2:
(Ⅲ)若M≧K对任意的b、c恒成立，试求k的最大值。
粤公网安备 44130202000953号