对于定义域为 的函数
的函数 ,若有常数M,使得对任意的
,若有常数M,使得对任意的 ,存在唯一的
,存在唯一的 满足等式
满足等式 ,则称M为函数
,则称M为函数 f (x)的“均值”.
f (x)的“均值”.
(1)判断1是否为函数 ≤
≤ ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
(2)若函数
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围;
(3)若函数 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数 的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
的“均值”情况(是否存在、个数、大小等)与区间I之间的关系,写出你的结论(不必证明).
说明:对于(3),将根据结论的完整性与一般性程度给予不同的评分
相关知识点
推荐套卷
 ,c=2,B=150°,求边b的长及S△.
,c=2,B=150°,求边b的长及S△.
 时,求a、b、c的值.
时,求a、b、c的值.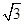 x+2=0的两根,角A、B满足2sin(A+B)-
x+2=0的两根,角A、B满足2sin(A+B)-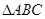 中, ⑴ 已知: acosB="bcosA" ,试判断
中, ⑴ 已知: acosB="bcosA" ,试判断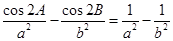 。
。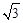 ,A=300,则角C及b.
,A=300,则角C及b. 粤公网安备 44130202000953号
粤公网安备 44130202000953号