（本小题满分12分）
设函数f(x)=lnx，g(x)=ax+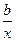
，函数f(x)的图像与x轴的交点也在函数g(x)的图像上，且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值；
(Ⅱ) 设x>0，试比较f(x)与g(x)的大小.
所对应的线性变换把点A(x，y)变成点A′(13，5)，试求M的逆矩阵及点A的坐标．
；(2)M＝
.
的特征值及相应的特征向量．
的特征值．
的特征多项式．推荐套卷
（本小题满分12分）
设函数f(x)=lnx，g(x)=ax+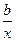，函数f(x)的图像与x轴的交点也在函数g(x)的图像上，且在此点处f(x)与g(x)有公切线.
(Ⅰ) 求a、b的值；
(Ⅱ) 设x>0，试比较f(x)与g(x)的大小.
粤公网安备 44130202000953号