某工厂对一批产品进行了抽样检测.右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是[96,106],样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36.
(1)求样本容量 ;
;
(2)求样本中净重大于或等于98克并且小于104克的产品的个数;
(3)求样本产品净重的中位数的估计值.(小数点后保留一位)
相关知识点
推荐套卷
 的焦点,离心率是
的焦点,离心率是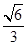
 为常数?若存在,求出点M的坐标;若不存在,请说明理由。
为常数?若存在,求出点M的坐标;若不存在,请说明理由。 (a>b>0)的左、右焦点分别是F1、F2,离心率为
(a>b>0)的左、右焦点分别是F1、F2,离心率为 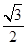 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为l.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为l. 为定值,并求出这个定值.
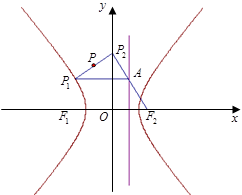
为定值,并求出这个定值. 为双曲线
为双曲线 (
( 为正常数)上任一点,
为正常数)上任一点, 为双曲线的右焦点,过
为双曲线的右焦点,过 作右准线的垂线,垂足为
作右准线的垂线,垂足为 ,连接
,连接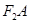 并延长交
并延长交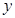 轴于
轴于 .
.
 的轨迹
的轨迹 的方程;
的方程; 轴交于
轴交于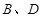 两点,在
两点,在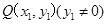 ,直线
,直线 分别交
分别交 两点.求证:以
两点.求证:以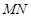 为直径的圆过两定点.
为直径的圆过两定点.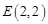 是抛物线
是抛物线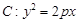 上一点,经过点
上一点,经过点 的直线
的直线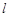 与抛物线
与抛物线 交于
交于 两点(不同于点
两点(不同于点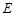 ),直线
),直线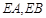 分别交直线
分别交直线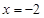 于点
于点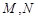 .
. 为原点,求证:
为原点,求证: 为定值.
为定值.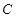 :
: ,
,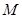 为直线
为直线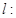
 上任意一点,过点
上任意一点,过点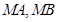 ,切点分别为
,切点分别为 ,
, .
.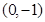 时,求过
时,求过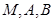 三点的圆的方程;
三点的圆的方程; 为直径的圆恒过点
为直径的圆恒过点 粤公网安备 44130202000953号
粤公网安备 44130202000953号