、(本小题满分12分)某市统计局就某地居民的月收入调查了10000人,他们的月收入均在 内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在
内.现根据所得数据画出了该样本的频率分布直方图如下.(每个分组包括左端点,不包括右端点,如第一组表示月收入在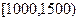 内)
内)
(1)求 某居民月收入在
某居民月收入在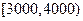 内的频率;
内的频率;
(2)根据该频率分布直方图估计居民的月收入的中位数; (3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在
(3)为了分析居民的月收入与年龄、职业等方面的关系,需再从这10000人中利用分层抽样的方法抽取100人作进一步分析,则应从月收入在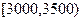 内的居民中抽取多少人?
内的居民中抽取多少人?
相关知识点
推荐套卷

 ,至少一个白球的概率为
,至少一个白球的概率为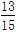 ,求摸出的两个球恰好红球白球各一个的概率.
,求摸出的两个球恰好红球白球各一个的概率.
 上点
上点 到焦点
到焦点 的距离为4.
的距离为4.
 ,
, 值;
值; ,
, 是抛物线上分别位于
是抛物线上分别位于 轴两侧的两个动点,且
轴两侧的两个动点,且 (其中
(其中 为坐标原点).求证:直线
为坐标原点).求证:直线 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标. 中,已知
中,已知 ,且
,且 (
( ).
). ,
, ,
, ;
; 粤公网安备 44130202000953号
粤公网安备 44130202000953号