（本小题满分12分）
在甲、乙等7个选手参加的一次演讲比赛中，采用抽签的方式随机确定每个选手的演出顺序（序号为1,2,……7），求：
（1）甲、乙两个选手的演出序号至少有一个为奇数的概率；
（2）甲、乙两选手之间的演讲选手个数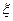
的分布列与期望.
相关试题
，两根为
.
求
的值.
关于x的表达式，并求
时，
为圆心的圆与
轴交于点
、
，与
轴交于点
，其中
的面积；
与圆
交于点
，若
，求圆
，
两点，且在y轴上截得的线段长为
，半径小于5。
∥
，且
，
，求直线相关知识点
推荐套卷
（本小题满分12分）
在甲、乙等7个选手参加的一次演讲比赛中，采用抽签的方式随机确定每个选手的演出顺序（序号为1,2,……7），求：
（1）甲、乙两个选手的演出序号至少有一个为奇数的概率；
（2）甲、乙两选手之间的演讲选手个数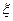的分布列与期望.
粤公网安备 44130202000953号