（本小题满分12分）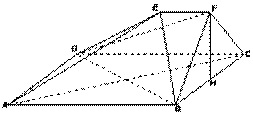
如图，在多面体ABCDEF中，ABCD是正方形，AB=2EF=2，
，EF⊥FB，∠BFC=
，BF=FC，H为BC的中点.
（Ⅰ）求证：
平面EDB；
（Ⅱ）求证：AC⊥平面EDB；
（Ⅲ）求四面体B—DEF的体积.
相关试题
．
，0＜β＜
，cos（
+α）=﹣
，sin（
+β）=
，求sin（α+β）的值．
|=3，|
|=5，
；
；
．
= ．推荐套卷
（本小题满分12分）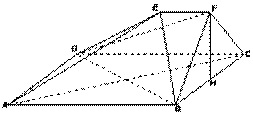
如图，在多面体ABCDEF中，ABCD是正方形，AB=2EF=2，，EF⊥FB，∠BFC=，BF=FC，H为BC的中点.
（Ⅰ）求证：平面EDB；
（Ⅱ）求证：AC⊥平面EDB；
（Ⅲ）求四面体B—DEF的体积.
粤公网安备 44130202000953号