.阅读材料,回答问题。
为了解方程
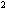 -4
-4 +3=0,我们可以把
+3=0,我们可以把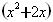 看成一个整体,并设x
看成一个整体,并设x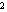 +2x=y,则原方程可化为y
+2x=y,则原方程可化为y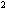 -4y+3=0①,解得y
-4y+3=0①,解得y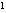 =1,y
=1,y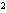 =3
=3
当y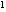 =1时,x
=1时,x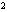 +2x=1,解得x
+2x=1,解得x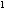 =
=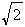 -1,x
-1,x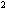 =-
=-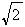 -1;
-1;
当y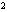 =3时,x
=3时,x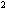 +2x=3,解得x
+2x=3,解得x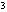 =-3,x
=-3,x =1。
=1。
故原方程的解为x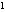 =
= -1,x
-1,x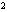 =-
=- -1,x
-1,x =-3,x
=-3,x =1
=1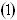 由原方程转化为方程①,这种方法,我们叫做换元法,换元的目的是
由原方程转化为方程①,这种方法,我们叫做换元法,换元的目的是 。
。 已知
已知
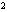 +
+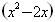 -2=0,求x
-2=0,求x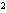 −2x的值。
−2x的值。
相关知识点
推荐套卷
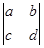 的意义是
的意义是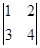 =1×4-2×3=-2,
=1×4-2×3=-2, =(-2)×5-4×3=-22.
=(-2)×5-4×3=-22.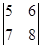 的值;
的值; 的值.
的值.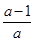 ÷
÷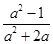 ,再选取一个合适的a值代入计算.
,再选取一个合适的a值代入计算.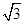 )2+(tan45°)-1.
)2+(tan45°)-1.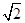 -1.
-1.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号