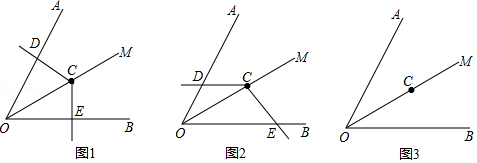
如图,已知 ,在 的平分线 上有一点 ,将一个 角的顶点与点 重合,它的两条边分别与直线 、 相交于点 、 .
(1)当 绕点 旋转到 与 垂直时(如图 ,请猜想 与 的数量关系,并说明理由;
(2)当 绕点 旋转到 与 不垂直时,到达图2的位置,(1)中的结论是否成立?并说明理由;
(3)当 绕点 旋转到 与 的反向延长线相交时,上述结论是否成立?请在图3中画出图形,若成立,请给于证明;若不成立,线段 、 与 之间又有怎样的数量关系?请写出你的猜想,不需证明.
相关知识点
推荐套卷
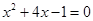
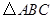 中,
中,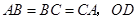 、
、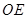 为
为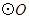 的半径,
的半径,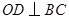 于
于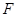 ,
, 于点
于点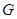 ,求证:
,求证:
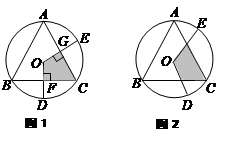
 阴影部分四边形
阴影部分四边形 的面积是
的面积是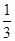 .
.
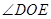 保持
保持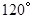 角度不变,求证:当
角度不变,求证:当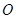 点旋转时,由两条半径
点旋转时,由两条半径 ,线段AB=180m,∠ABD=150°.
,线段AB=180m,∠ABD=150°.
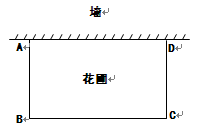
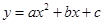 (
(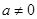 ),当
),当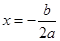 时,
时,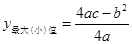 )
) 粤公网安备 44130202000953号
粤公网安备 44130202000953号