(本小题满分12分)
某中学经市人民政府批准建分校,工程从2010年底开工到2013年底完工,工程分三期完成。经过初步招投标淘汰后,确定只由甲、乙两家建筑公司承建,且每期工程由两公司之一独立承 建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为
建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为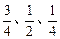 .
.
(1)求甲、乙两公司各至少获得一期工程的概率;
(2)求甲公司获得工程期数 的分布列和数学期望
的分布列和数学期望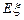 .
.
推荐套卷
(本小题满分12分)
某中学经市人民政府批准建分校,工程从2010年底开工到2013年底完工,工程分三期完成。经过初步招投标淘汰后,确定只由甲、乙两家建筑公司承建,且每期工程由两公司之一独立承 建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为
建,必须在建完前一期工程后再建后一期工程。已知甲公司获得第一期、第二期、第三期工程承包权的概率分别为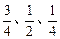 .
.
(1)求甲、乙两公司各至少获得一期工程的概率;
(2)求甲公司获得工程期数 的分布列和数学期望
的分布列和数学期望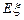 .
.