如图,在平面直角坐标系xOy中,已知F1,F2分别是椭圆E: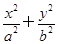 =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且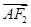 +5
+5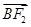 =0.
=0.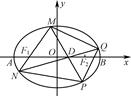
(1)求椭圆E的离心率; (2)已知点D(1,0)为线段OF2的中点,M为椭圆E上的动点(异于点A、B),连结MF1并延长交椭圆E于点N,连结MD、ND并分别延长交椭圆E于点P、Q,连结PQ,设直线MN、PQ的斜率存在且分别为k1、k2,试问是否存在常数λ,使得k1+λk2=0恒成立?若存在,求出λ的值;若不存在,说明理由.
推荐套卷
如图,在平面直角坐标系xOy中,已知F1,F2分别是椭圆E: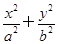 =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且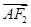 +5
+5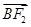 =0.
=0.
(1)求椭圆E的离心率; (2)已知点D(1,0)为线段OF2的中点,M为椭圆E上的动点(异于点A、B),连结MF1并延长交椭圆E于点N,连结MD、ND并分别延长交椭圆E于点P、Q,连结PQ,设直线MN、PQ的斜率存在且分别为k1、k2,试问是否存在常数λ,使得k1+λk2=0恒成立?若存在,求出λ的值;若不存在,说明理由.