在美化校园的植树活动中,某同学共种了6棵树,各棵树的成活与否是相互独立的, 每棵树成活的概率均为p.已知该同学所种树中有3棵成活的概率为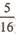 .
.
(I)求p的值;
(II)若有3棵或3棵以上的树未成活,则需要补种,求需要补种的概率;
(Ⅲ)设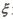 为成活树的棵数,求
为成活树的棵数,求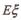 .
.
推荐套卷
在美化校园的植树活动中,某同学共种了6棵树,各棵树的成活与否是相互独立的, 每棵树成活的概率均为p.已知该同学所种树中有3棵成活的概率为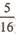 .
.
(I)求p的值;
(II)若有3棵或3棵以上的树未成活,则需要补种,求需要补种的概率;
(Ⅲ)设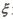 为成活树的棵数,求
为成活树的棵数,求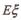 .
.