如图，椭圆C0：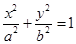
(a＞b＞0，a，b为常数)，动圆C1：x2＋y2＝t12，b＜t1＜a．点A1，A2分别为C0的左，右顶点，C1与C0相交于A，B，C，D四点．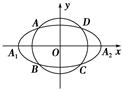
(1)求直线AA1与直线A2B交点M的轨迹方程；
(2)设动圆C2：x2＋y2＝t22与C0相交于A′，B′，C′，D′四点，其中b＜t2＜a，t1≠t2．若矩形ABCD与矩形A′B′C′D′的面积相等，证明：t12＋t22为定值．
相关试题
的最小值为
.
求
的值及此时
的最大值.
与
的夹角为
，且
，
，求实数
的值及
与
的夹角
.
的一个周期的图象，如图（1）求
的解析式（2）若函数
与
对称，求
的值；
的值.
的左,右焦点为
，
，（１，
）为椭圆上一点，椭圆的
轴的对称点记为Ｍ，设
．
；
求|ＰＱ|的取值范围推荐套卷
如图，椭圆C0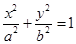：(a＞b＞0，a，b为常数)，动圆C1：x2＋y2＝t12，b＜t1＜a．点A1，A2分别为C0的左，右顶点，C1与C0相交于A，B，C，D四点．
(1)求直线AA1与直线A2B交点M的轨迹方程；
(2)设动圆C2：x2＋y2＝t22与C0相交于A′，B′，C′，D′四点，其中b＜t2＜a，t1≠t2．若矩形ABCD与矩形A′B′C′D′的面积相等，证明：t12＋t22为定值．
粤公网安备 44130202000953号