如图，正方形ABCD内接于椭圆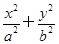
＝1(a＞b＞0)，且它的四条边与坐标轴平行，正方形MNPQ的顶点M、N在椭圆上，顶点P、Q在正方形的边AB上，且A、M都在第一象限．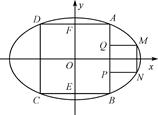
(1)若正方形ABCD的边长为4，且与y轴交于E、F两点，正方形MNPQ的边长为2.
①求证：直线AM与△ABE的外接圆相切；
②求椭圆的标准方程；
(2)设椭圆的离心率为e，直线AM的斜率为k，求证：2e2－k是定值．
相关试题
,集合
（2）求
＋
.
，使f(x0)＝x0.
都有|f(x)|≤1成立，试求a的取值范围．
上的最大值．推荐套卷
如图，正方形ABCD内接于椭圆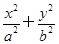＝1(a＞b＞0)，且它的四条边与坐标轴平行，正方形MNPQ的顶点M、N在椭圆上，顶点P、Q在正方形的边AB上，且A、M都在第一象限．
(1)若正方形ABCD的边长为4，且与y轴交于E、F两点，正方形MNPQ的边长为2.
①求证：直线AM与△ABE的外接圆相切；
②求椭圆的标准方程；
(2)设椭圆的离心率为e，直线AM的斜率为k，求证：2e2－k是定值．
粤公网安备 44130202000953号