（本小题满分14分）
建造一容积为8
深为2m的长方体形无盖水池，每
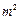池底和池壁造价各为120元和80元.
（1）求总造价关于一边长x的函数解析式，并指出该函数的定义域；
（2）判断（1）中函数在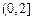
和
上的单调性；
（3）如何设计水池尺寸，才能使总造价最低；
相关试题
的前
项和为
，
；
，
的值；
中，
，求数列
为数列
项和，
，
，求数列
中，
且
成等比数列，求数列
．
为数列
的前
项和，求下列数列
；⑵
.
和
满足：
，
，
，
为实数，
.
，数列
为数列
项和，是否存在实数
？相关知识点
推荐套卷
（本小题满分14分）
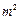建造一容积为8深为2m的长方体形无盖水池，每池底和池壁造价各为120元和80元.
（1）求总造价关于一边长x的函数解析式，并指出该函数的定义域；
（2）判断（1）中函数在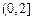和上的单调性；
（3）如何设计水池尺寸，才能使总造价最低；
粤公网安备 44130202000953号