一个盒子中装有大小相同的小球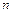
个，在小球上分别标有1，2，3，
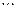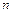,的号码，已知从盒子中随机的取出两个球，两球的号码最大值为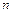的概率为
，
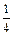（Ⅰ）问：盒子中装有几个小球？
（Ⅱ）现从盒子中随机的取出4个球，记所取4个球的号码中，连续自然数的个数的最大值为随机变量
（如取2468时，=1；取1246时，=2，取1235时，=3），
（ⅰ）求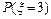
的值；（ⅱ）求随机变量的分
布列及均值．
相关试题
，其图象过点
的值；
图象上各点向左平移
个单位长度，得到函数
的图象，求函数
在
上的单调递增区间.
，函数
·
，
．
的值； 
，求
的值． 
，求函数f(x)的值域；
取得最大值时，求自变量
的取值集合；
满足
及 
的值．
都为锐角，
，求
与
的值
的值推荐套卷
一个盒子中装有大小相同的小球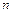个，在小球上分别标有1，2，3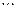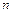，,的号码，已知从盒子中随机的取出两个球，两球的号码最大值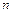为的概率为，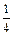
（Ⅰ）问：盒子中装有几个小球？
（Ⅱ）现从盒子中随机的取出4个球，记所取4个球的号码中，连续自然数的个数的最大值为随机变量（如取2468时，=1；取1246时，=2，取1235时，=3），
（ⅰ）求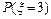的值；（ⅱ）求随机变量的分布列及均值．
粤公网安备 44130202000953号