(1)(本小题满分7分)
选修4-4:矩阵与变换
已知矩阵
 ,A的一个特征值
,A的一个特征值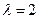 ,其对应的特征向量是
,其对应的特征向量是 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求直线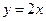 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程
(2)
(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: ,
, 求直线l与曲线C相交所成的弦的弦长.
求直线l与曲线C相交所成的弦的弦长.
((3)(本小题满分7分)
选修4-5:不等式选讲解不等式∣2x-1∣<∣x∣+1
推荐套卷
(1)(本小题满分7分)
选修4-4:矩阵与变换
已知矩阵
 ,A的一个特征值
,A的一个特征值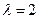 ,其对应的特征向量是
,其对应的特征向量是 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)求直线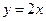 在矩阵M所对应的线性变换下的像的方程
在矩阵M所对应的线性变换下的像的方程
(2)
(本小题满分7分)选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: ,
, 求直线l与曲线C相交所成的弦的弦长.
求直线l与曲线C相交所成的弦的弦长.
((3)(本小题满分7分)
选修4-5:不等式选讲解不等式∣2x-1∣<∣x∣+1