(本小题满分12分)已知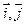 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设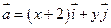 ,
, 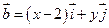 且满足
且满足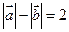
(1)、求点P (x,y)的轨迹E的方程.
(x,y)的轨迹E的方程.
(2)、若直线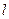 过点
过点 且法向量为
且法向量为 ,直线与轨迹E交于
,直线与轨迹E交于 两点.点
两点.点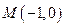 ,无论直线
,无论直线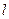 绕点
绕点 怎样转动,
怎样转动, 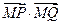 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数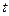 的取值范围;
的取值范围;
推荐套卷
(本小题满分12分)已知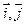 是x,y轴正方向的单位向量,设
是x,y轴正方向的单位向量,设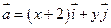 ,
, 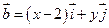 且满足
且满足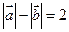
(1)、求点P (x,y)的轨迹E的方程.
(x,y)的轨迹E的方程.
(2)、若直线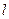 过点
过点 且法向量为
且法向量为 ,直线与轨迹E交于
,直线与轨迹E交于 两点.点
两点.点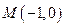 ,无论直线
,无论直线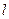 绕点
绕点 怎样转动,
怎样转动, 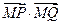 是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数
是否为定值?如果是,求出定值;如果不是,请说明理由.并求实数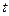 的取值范围;
的取值范围;